پاسخ جزئي به پرسشي بزرگ پيرامون اعداد اول

دو رياضي‌دان در تاريخ ۷ سپتامبر اثبات خود براي مدلي از مشهورترين مسائل رياضي را ارائه دادند. نتايج اين اثبات، چشم‌انداز جديدي به مطالعه فرضيه‌ي اعداد اول دوقلو باز كرده است كه بيش از يك قرن ذهن رياضيدان‌ها را به خود مشغول كرده است. اين فرضيه راهگشاي پيچيده‌ترين مسائل علم حساب خواهد بود. به‌گفته‌ي جيمز ماينارد، رياضيدان دانشگاه آكسفورد:

مدت‌ها در حال درجا زدن بوديم و ايده‌اي براي حل اين مسئله نداشتيم بنابراين وقتي ايده‌هاي جديد مطرح شدند ناخودآگاه هيجان‌زده شديم.

اعداد اول دوقلو، به زوج اعداد اول با تفاضل ۲ گفته مي‌شود. زوج‌هاي عددي ۵ و ۷ يا ۱۷ و ۱۹ از اعداد اول دوقلو هستند. براساس اين فرضيه بي‌نهايت زوج عدد اول دوقلو در ميان اعداد صحيح وجود دارد. رياضي‌دان‌ها در زمينه‌ي حل اين فرضيه‌ در دهه‌ي گذشته به شكل چشمگيري پيشرفت كرده‌اند اما تاكنون قادر به حل آن نشده بودند.

ويل ساوين از دانشگاه كلمبيا و مارك شوسترمان از دانشگاه ويسكانسين ماديسون در اثبات جديد خود، فرضيه‌ي اعداد اول دوقلو را براي محدوده‌ي كوچكتري از اعداد حل كردند. آن‌ها اين فرضيه را براي يك مجموعه از دستگاه‌هاي عددي متناهي ثابت كردند كه ممكن است دربردارنده‌ي مجموعه‌ي محدودي از اعداد اول دوقلو باشد.

به دستگاه‌هاي عددي فوق، «ميدان‌هاي متناهي» گفته مي‌شود. با اينكه اين مجموعه از انديشه متخصصين اندازه كوچك است اما مي‌توان اغلب ويژگي‌هاي اعداد صحيح نامتناهي را در آن يافت. رياضي‌دان‌ها در تلاش‌اند به سؤال‌هاي رياضي روي ميدان‌هاي متناهي پاسخ دهند و نتايج را به اعداد صحيح هم تعميم دهند. به‌گفته‌ي ماينارد:

براي رسيدن به رويايي نهايي در ابتدا بايد به درك مناسبي از دنياي ميدان‌هاي متناهي رسيد سپس اين نتيجه مي‌تواند راه خود را به دنياي اعداد صحيح باز كند

ساوين و شوسترمان علاوه بر اثبات فرضيه‌ي اعداد اول دوقلو به نتيجه‌ي فراگيرتري درباره‌ي رفتار اعداد اول در دستگاه‌هاي عددي كوچك رسيده‌اند. آن‌ها به محاسبه‌ي تعداد تكرار اعداد اول دوقلو روي بازه‌هاي كوچك‌تر پرداختند. از اين نتيجه مي‌توان براي كنترل دقيق‌تر اعداد دوقلوي اول استفاده كرد. رياضي‌دان‌ها اميدوار هستند براي اعداد ترتيبي هم به نتايج مشابهي برسند؛ آن‌ها اثبات جديد را براي اعداد اول روي محور حقيقي مطالعه خواهند كرد.

نوع جديدي از اعداد اول

براساس مشهورترين پيش‌بيني فرضيه‌ي اعداد اول دوقلو مي‌توان بي‌نهايت زوج عدد اول با تفاضل ۲ پيدا كرد؛ اما اين فرضيه فراتر از صرفا تفاضل ۲ است. براي مثال مي‌توان بي‌نهايت زوج عدد اول با اختلاف ۴ (مانند ۳ و ۷) يا ۱۴ (۲۹۳ و ۳۰۷) و به‌طور كلي تفاضل دلخواه بيشتر از ۲ پيدا كرد.

آلفونس دي پوليگناك ، رياضي‌دان فرانسوي، در سال ۱۸۴۹ از اين فرضيه به شكل امروزي آن استفاده كرد. رياضي‌دان‌ها در طول ۱۶۰ سال پس از آلفونس پيشرفت كمي در اثبات اين فرضيه داشتند؛ اما نهايتا در سال ۲۰۱۳ اين سد شكسته شد. درهمان سال ييتانگ ژانگ ثابت كرد بي‌نهايت زوج عدد اول با تفاضل حداكثر ۷۰ ميليون وجود دارد. سال بعد از اين كشف رياضي‌دان‌هاي ديگري از جمله ماينارد و تري تائو شكاف اعداد اول را به شكل چشمگيري كاهش دادند. آخرين اثبات، وجود بي‌نهايت زوج عدد اول با اختلاف حداكثر ۲۴۶ بود.

در مرحله‌ي بعدي محاسبات روي صفحه‌ي ساعت انجام مي‌شوند. براي مثال ۳+۴ در دستگاه عددي متناهي با پنج عدد چيست؟ از ۴ شروع كنيد پس از طي سه فاصله اطراف ساعت به عدد ۲ مي‌رسيد. تفريق، ضرب و تقسيم هم عملكرد مشابهي دارند.

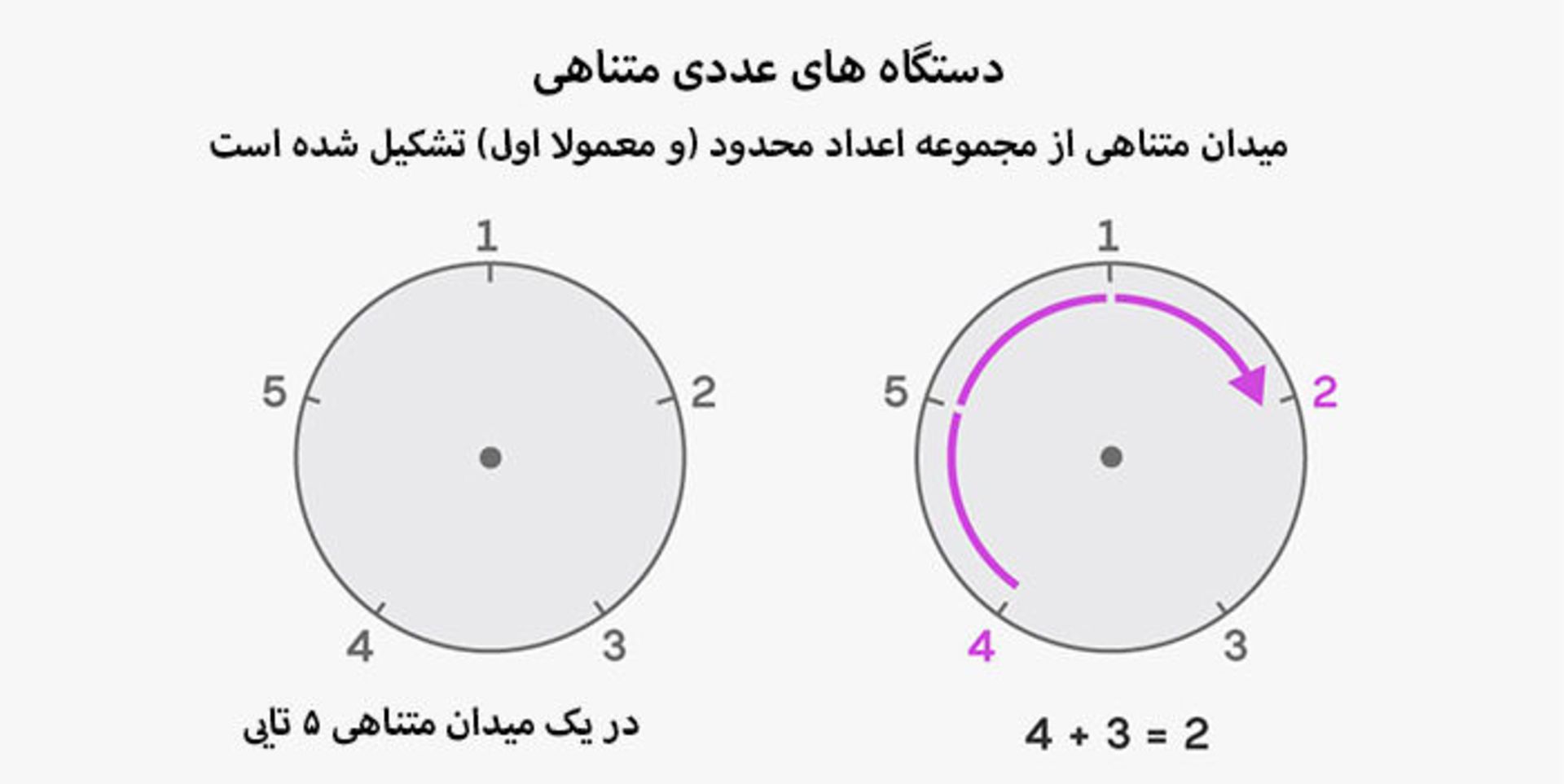
روش ميدان‌هاي متناهي تنها يك دستاورد دارد. مفهوم رايج اعداد اول در ميدان‌هاي متناهي شكل متفاوتي به خود مي‌گيرد. در يك ميدان متناهي هر عدد بر عدد ديگر بخش‌پذير است. براي مثال، ۷ معمولا بر ۳ بخش‌پذير نيست؛ اما در ميدان متناهي با پنج عنصر، چنين رابطه‌اي وجود دارد. به همين دليل در اين ميدان متناهي، ۷ مشابه ۱۲ است هر دو در صفحه‌ي ساعت روي ۲ قرار مي‌گيرند؛ بنابراين ۷ تقسيم بر ۳ مشابه ۱۲ تقسيم بر ۳ است؛ و جواب ۱۲ تقسيم بر ۳ برابر با ۴ است.

به همين دليل، فرضيه‌ي اعداد دوقلوي اول براي ميدان‌هاي متناهي درباره‌ي چندجمله‌اي‌هاي اول مثل x۲+1 صدق مي‌كند. براي مثال، فرض كنيد ميدان متناهي شما شامل اعداد ۱، ۲ و ۳ است. يك چندجمله‌اي در اين ميدان متناهي اعدادي را به‌عنوان ضريب دربردارد و چندجمله‌اي اول، قابل تجزيه بر چندجمله‌اي‌هاي كوچك‌تر نيست؛ بنابراين x۲+x +۲ اول است زيرا نمي‌توان آن را تجزيه كرد اما x۲-۱ اول نيست زيرا به (x+۱) و (x-۱) قابل تجزيه است.

در چندجمله‌اي‌هاي اول، يافتن چندجمله‌اي‌هاي اول دوقلو هم امري عادي است. چندجمله‌اي اول دوقلو به يك زوج چندجمله‌اي اطلاق مي‌شود كه هم اول باشند و هم اختلاف ثابتي با يكديگر داشته باشند. براي مثال چندجمله‌اي x۲+x +۲ مشابه x۲+۲x+۲ اول است. هر دو داراي اختلاف x هستند (براي رسيدن به چندجمله‌اي دوم، x را به چندجمله‌اي اول اضافه كنيد). طبق فرضيه‌ي اعداد اول دوقلو براي ميدان‌هاي متناهي، بي‌نهايت زوج چندجمله‌اي اول دوقلو وجود دارد كه داراي اختلاف x يا اختلاف‌هاي دلخواه ديگر است.

برش‌هاي تميز

شايد چندجمله‌اي‌هاي اول و ميدان‌هاي متناهي به انديشه متخصصين مصنوعي برسند و به‌طور كلي متخصصد كمي در علم اعداد داشته باشند اما مشابه يك شبيه‌ساز طوفان عمل مي‌كنند؛ جهاني مستقل كه از آن مي‌توان به انديشه متخصصينات‌هايي درباره‌ي پديده‌هاي جهان واقعي رسيد. به‌گفته‌ي شوسترمان:

براساس يك قياس كهن بين اعداد صحيح و چندجمله‌اي‌ها، مي‌توان مسائل مربوط به اعداد صحيح را كه معمولا مسائل بسيار دشواري هستند به مسائل چندجمله‌اي تبديل كرد كه دشوار ولي قابل كنترل هستند»

آندره وي در دهه‌ي ۱۹۴۰ روشي دقيق براي ترجمه‌ي رياضيات دستگاه‌هاي عددي كوچك به رياضيات اعداد صحيح ابداع كرد؛ از همين نقطه ميدان‌هاي متناهي در مركز توجه قرار گرفتند. او مهم‌ترين مسئله‌ي رياضي يعني فرضيه‌ي ريمان را براي منحني‌هاي روي ميدان‌هاي متناهي اثبات كرد (مسئله‌اي كه به‌عنوان فرضيه‌ي ريماني هندسي هم شناخته مي‌شود). اين اثبات همراه‌با يك مجموعه از حدس و گمان‌هاي وي، ميدان‌هاي متناهي را به‌عنوان چشم‌اندازي غني براي اكتشافات رياضي تبديل كرده است.

براساس انديشه متخصصينات كليدي آندره وي، در ميدان‌هاي متناهي مي‌توان از روش‌هاي هندسي براي پاسخگويي به مسئله‌هاي عددي استفاده كرد. شوسترمان مي‌گويد: «اين ويژگي خاص ميدان‌هاي متناهي است كه مي‌توان براي حل بسياري از مسائل به بازتعريف هندسي آن‌ها پرداخت.»

اما حتي ساده‌ترين ميدان متناهي هم داراي تعدادي نامتناهي چندجمله‌اي است. مي‌توان با افزايش اندازه‌ي بزرگ‌ترين نما يا درجه‌ي عبارت، چندجمله‌اي‌هاي دقيق‌تري ساخت. براي مثال چندجمله‌اي x۲-۳x-۱ به‌صورت يك نقطه در فضاي سه‌بعدي نمايش داده مي‌شود. چندجمله‌اي ۳x۷+۲x۶+۲x۵-۲x۴-۳x۳+x۲-۲x+۳ به‌صورت يك نقطه در فضاي هشت‌بعدي نمايش داده مي‌شود.

فضاي هندسي در فرضيه‌ي جديدشامل كل چندجمله‌اي‌ها با يك درجه‌ي مشخص براي يك ميدان متناهي مشخص است. حالا اين سؤال مطرح مي‌شود: راهي براي جداسازي كل نقاط نمايش‌دهنده‌ي چندجمله‌اي‌هاي اول وجود دارد؟ استراتژي ساوين و شوسترمان تقسيم فضا به دو بخش است. يكي از بخش‌ها شامل تمام چندجمله‌اي‌ها با تعداد ضريب زوج و ديگري شامل چندجمله‌اي‌ها با تعداد ضريب فرد است.

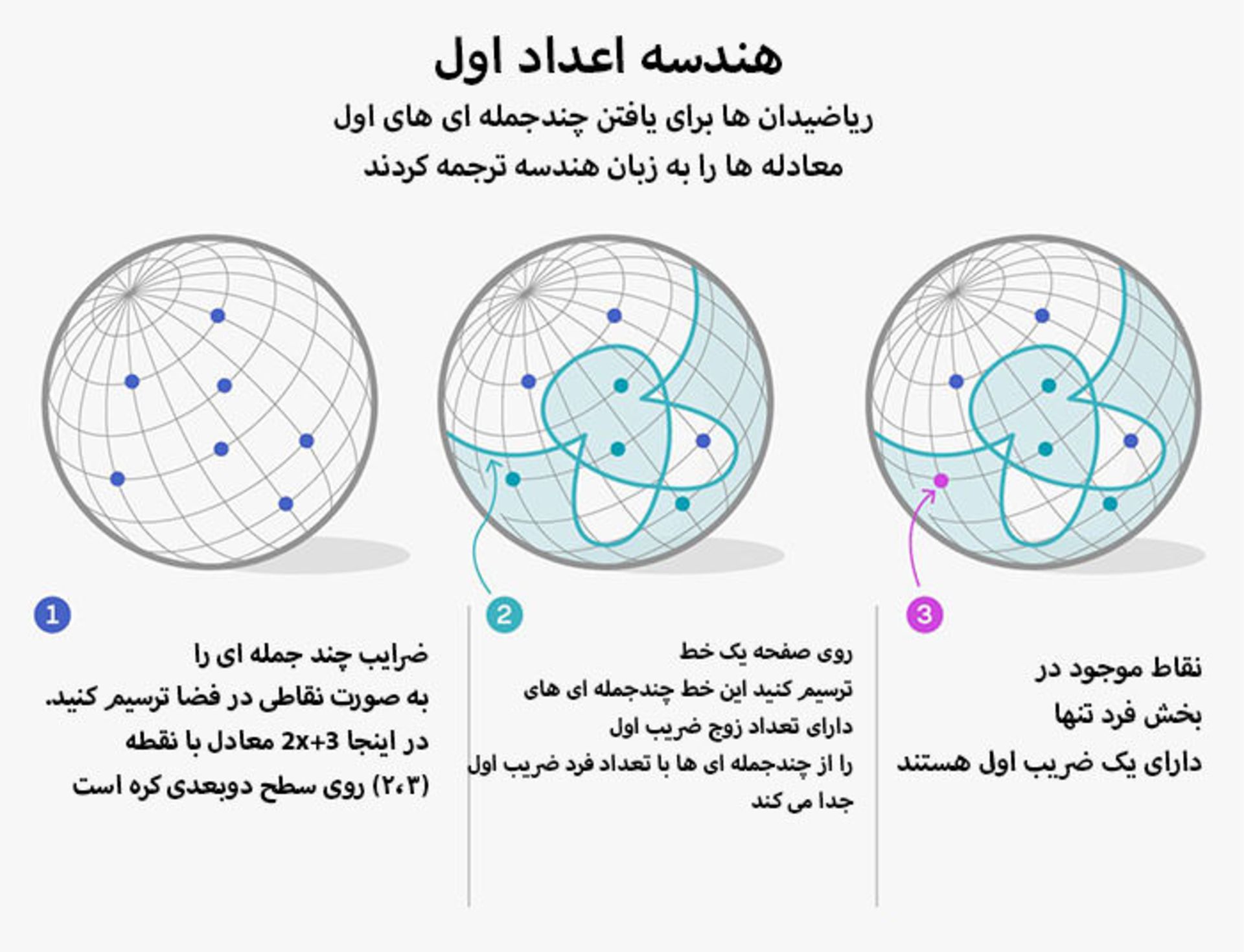
به اين ترتيب حل مسئله با تقسيم‌بندي يادشده آسان‌تر مي‌شود. فرضيه‌ي اعداد اول دوقلو براي ميدان‌هاي متناهي با ضريب يك صدق مي‌كند (همان‌طور كه عدد اول داراي يك ضريب مستقل يعني خود آن عدد است)؛ و از آنجا كه عدد ۱ فرد است مي‌توان بخشي از فضا با ضريب‌هاي زوج را كاملا ناديده گرفت.

ترفند اصلي حل مسئله در تقسيم است. يك منحني يك‌بعدي مي‌تواند فضايي دوبعدي را به دو قسمت تقسيم كند. براي مثال خط استوا سطح زمين را به دو قسمت تقسيم مي‌كند. به همين ترتيب مي‌توان فضاهاي با ابعاد بالاتر را به‌وسيله‌ي سطوحي با ابعاد كمتر تقسيم كرد.

از طرفي شكل‌هايي با ابعاد كمتر كه فضاهاي چندجمله‌اي را تقسيم مي‌كنند مانند استوا واضح نيستند. چنين اشيايي براساس فرمولي رياضي به نام تابع موبيوس ترسيم مي‌شوند كه يك چندجمله‌اي را به‌عنوان ورودي دريافت مي‌كند و در صورتي كه تعداد ضريب‌هاي اول چندجمله‌اي زوج باشد، خروجي ۱، در صورتي كه تعداد ضريب‌هاي چندجمله‌اي فرد باشد، منفي ۱ و در صورتي كه صرفا داراي يك ضريب تكراري باشد صفر را برمي‌گرداند (براي مثال ۱۶ را مي‌توان به‌صورت ۲*۲*۲*۲ به دست آورد).

ساوين و شوسترمان پس از طبقه‌بندي چندجمله‌اي‌ها براساس تعداد ضريب اول فرد (سخت‌ترين مرحله)، بايد مشخص مي‌كردند كدام يك از چندجمله‌اي‌ها اول و كدام يك دوقلوي اول هستند. آن‌ها براي رسيدن به اين هدف از فرمول‌هاي متعددي استفاده كردند كه معمولا رياضي‌دان‌ها براي مطالعه اعداد اول در ميان اعداد طبيعي به كار مي‌برند. ساوين و شوسترمان از روش خود براي اثبات دو نتيجه‌ي عمده درباره‌ي تعداد زيادي از زوج چندجمله‌اي‌هاي اول دوقلو با تفاضل مشخص استفاده كردند.

علاوه بر اين اثبات جديد تعداد دقيق چندجمله‌اي‌هاي اول قابل انتظار در ميان چندجمله‌اي‌هايي از يك درجه‌ي مشخص را نمايش مي‌دهد. اين دستاورد هم ارز دستيابي به تعداد اعداد اول دوقلو در بازه‌اي طولاني روي محور اعداد حقيقي است؛ نتيجه‌اي رويايي براي رياضي‌دان‌ها. زيو رودنيك رياضي‌دان مي‌گويد: «اين اولين اثباتي است كه قياسي كمي از مقدار قابل انتظار روي بازه‌اي از اعداد صحيح را نمايش مي‌دهد و قبلا چنين نتيجه‌اي به دست نيامده است.»

با وجود گذشت تقريبا ۸۰ سال از اثبات فرضيه‌ي ريمان در منحني‌هاي ميدان متناهي توسط آندره وي، ساوين و شوسترمان نشان دادند كه اين انديشه متخصصينيه امروزه هم متخصصد دارد. امروزه رياضي‌دان‌ها پژوهش خود را روي فرضيه‌ي ساوين و شوسترمان متمركز كرده‌اند؛ اين انديشه متخصصينيه مي‌تواند الهام‌بخش دانشمندان ديگر باشد.