كشف راه‌حلي دقيق براي مسئله رياضي ساده‌اي پس از قرن‌ها

اين مسئله ساده به‌انديشه متخصصين مي‌رسد: حصاري مدوّر را در انديشه متخصصين بگيريد كه زمين چمن را محصور كرده است. اگر بزي را با طناب به داخل حصار ببنديد، چقدر طناب نياز داريد تا حيوان بتواند دقيقا به نيمي از زمين دسترسي پيدا كند؟ به‌انديشه متخصصين مي‌رسد مسئله‌ي مذكور به‌سادگي مسائل دبيرستان باشد؛ اما رياضي‌دانان و علاقه‌مندان رياضي بيش از ۲۷۰ سال به‌دنبال راه‌حلي ساده براي اين مسئله بودند و با اينكه توانستند راه‌حل‌هايي برايش پيدا كنند، پاسخ‌ها ناقص و مبهم بودند. مارك ميرسون، رياضي‌دان آكادمي نيروي دريايي ايالات متحده‌ي آمريكا، درباره‌ي اين موضوع مي‌گويد:

حتي پس از ۲۷۰ سال، هنوز كسي پاسخ دقيقي براي مسئله‌ي بز محصور پيدا نكرده است. راه‌‌حل فقط به‌صورت تقريبي ارائه شده است.

در آغاز سال رياضيداني آلماني به نام اينگو اوليسچ در نهايت موفق به پيشرفت در حل اين مسئله شد و راه‌حلي دقيق را براي آن پيدا كرد. گرچه اين راه‌حل از انديشه متخصصينات خواننده چندان مناسب و مستقيم نبود. بااين‌حال به گفته‌ي مايكل هريسون، رياضيدن دانشگاه كارنيگ ملون:

پاسخ اوليسچ اولين پاسخ دقيق براي طول طناب است و پيشرفت مهمي به شمار مي‌رود.

البته دستيابي به پاسخ دقيق براي مسئله‌ي بز محصور متون رياضي يا پژوهش‌ها را متحول نخواهد كرد؛ زيرا به‌عقيده‌ي اوليسچ اين مسئله، مسئله‌اي منزوي است و ربط زيادي به مسائل ديگر ندارد و در انديشه متخصصينيه‌ي رياضيات تعبيه نشده است؛ اما مسائل سرگرم‌كننده‌ي اين‌چنيني مي‌توانند ايده‌هاي جديد رياضي را ارائه كنند و به پژوهشگران در يافتن راه‌حل‌هاي جديد براي مسائل ديگر كمك كنند.

اولين مسئله‌‌ي مشابه بز محصور در سال ۱۷۴۸ در مجله‌ي The Ladies Diary منتشر شد. در سناريو اصلي مسئله، اسبي براي غذاخوردن در پارك جنتلمن محصور شده است. در اين نمونه، اسب خارج از حصار قرار دارد. اگر طول طناب به‌اندازه‌ي محيط حصار باشد، حداكثر مساحت تغذيه‌ي اسب چقدر است؟ اين نسخه در گروه مسئله‌ي «خارجي» دسته‌بندي شده است؛ زيرا اسب خارج از حصار دايره‌اي قرار دارد. پاسخ به مسئله‌ي يادشده در نسخه‌ي ۱۷۴۹ مجله‌ي Diary منتشر شد. اين مسئله را شخصي به‌نام آقاي هيت با استفاده از جدول لگاريتمي حل كرد. پاسخ هيت ۷۶۲۵۷.۸۶ يارد مربع براي طناب ۱۶۰ ياردي بود كه تقريبا راه‌حلي دقيق به‌شمار مي‌رفت.

در سال ۱۸۹۴، مسئله دوباره در اولين نسخه‌ از ماهنامه‌ي رياضي آمريكايي با عنوان مسئله‌ي چرنده‌اي در حصار مطرح شد؛ ولي اين بار بدون اشاره‌ به حيوانات مزرعه. اين نوع مسئله در دسته‌ي فضاي داخلي قرار مي‌گيرد و دشوارتر از مسئله‌ي خارج از حصار است. در مسئله‌ي خارج از حصار، حل مسئله با شعاع دايره و طول طناب آغاز و مساحت محاسبه مي‌شود. همچنين، مي‌توان ازطريق انتگرال مسئله را حل كرد.

در سال‌هاي بعد، ماهنامه‌ي رياضي انواع مختلفي از مسئله‌ي فضاي داخلي را منتشر كرد كه به‌جاي بز، از اسب نام برده بود و حصارها هم به شكل‌هاي دايره و مربع و بيضي بودند؛ اما در دهه‌ي ۱۹۶۰، به‌دلايل نامعلومي بزها جاي اسب‌هاي را در مسئله‌ي چرنده در حصار گرفتند. اين در حالي است ‌كه به‌گفته‌ي مارشال فريسرِ رياضي‌دان، بزها معمولا كمتر تابع افسار هستند.

در سال ۱۹۸۴، فريزر مسئله را از حالت مسطح خارج كرد و آن را به ابعاد بزرگ‌تر تعميم داد. او مسئله را به اين صورت تغيير داد: چقدر طناب لازم است تا بز بتواند دقيقا نيمي از حجم كره‌ي n بعدي بچرد؟ در اين مسئله، n به‌سمت بي‌نهايت ميل مي‌كند. ميرسون خطايي منطقي را در اين مسئله كشف كرد و همان سال اشتباه فريزر را تصحيح كرد؛ اما به يك نتيجه رسيد: با ميل n به مست بي‌نهايت، نسبت طناب افسار به شعاع كره به راديكال دو مي‌رسد.

به‌گفته‌ي ميرسون، روش به‌ظاهر پيچيده‌ي يادشده براي حل مسئله‌ در فضاي چند‌بُعدي، يافتن راه‌حل را آسان‌تر مي‌سازد. او مي‌افزايد:

در ابعاد بي‌نهايت به پاسخ شفافي مي‌رسيم؛ درحالي‌كه در دو بُعد چنين پاسخ واضحي وجود ندارد.

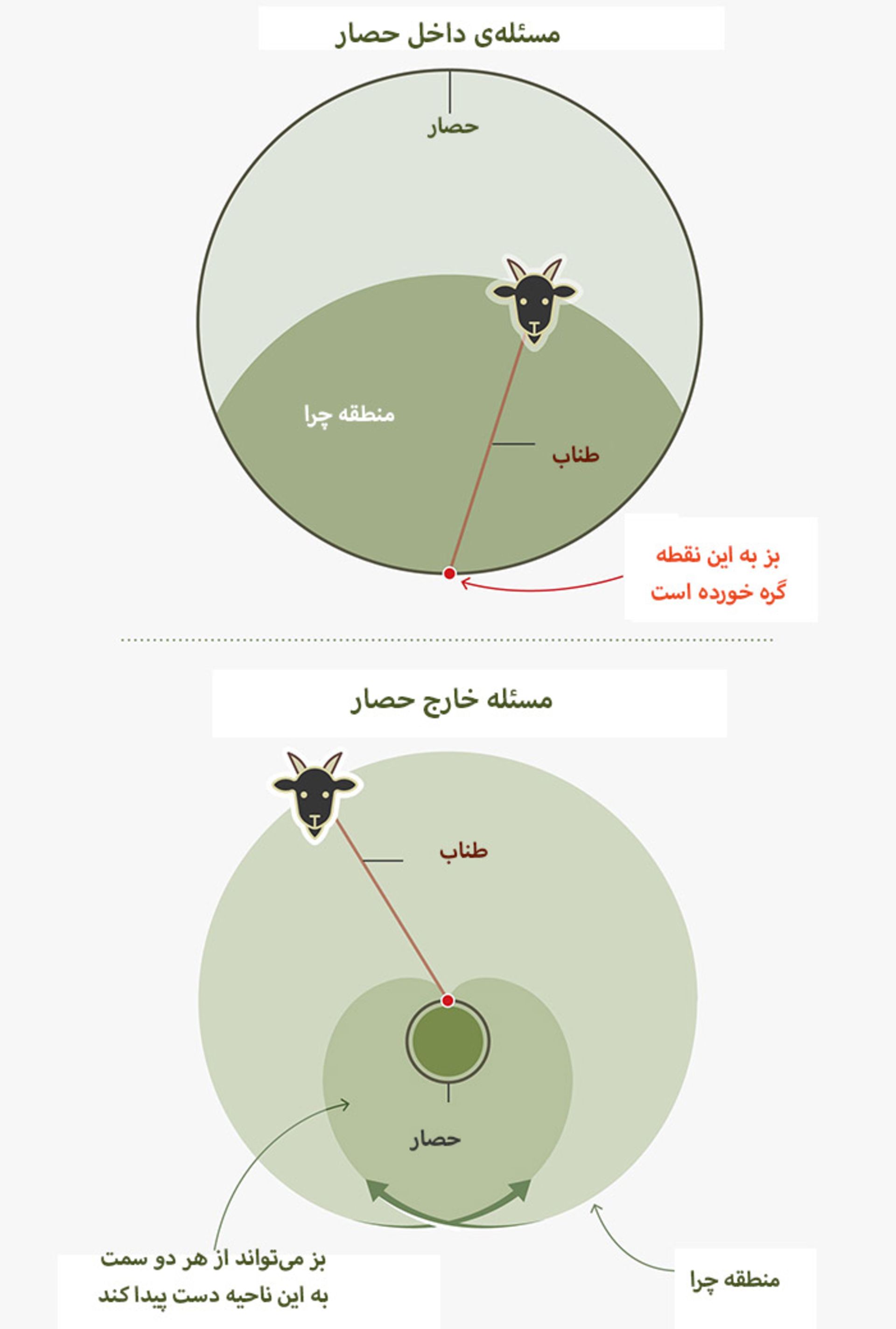
مسئله‌ي بز محصور به دو شكل مطرح مي‌شود؛ اما هميشه با بزي آغاز مي‌شود كه به حصاري مدوّر بسته شده است. نسخه‌ي داخلي بدين‌صورت مطرح مي‌شود: اگر بز بخواهد دقيقا به نيمي از ناحيه‌ي محصور دسترسي پيدا كند، چقدر طناب لازم است؟ نسخه‌ي خارجي بدين‌ترتيب مطرح مي‌شود: با وجود طول مشخص طناب و محيط حصار، بز به چقدر از مساحت خارجي دسترسي پيدا خواهد كرد؟ گفتني است در اين نمونه، طول طناب برابر با محيط حصار است.

مايكل هافمن، از رياضي‌دانان آكادمي نيروي دريايي ايالات متحده‌ي آمريكا، در سال ۱۹۹۸ مسئله را به‌ گونه‌اي ديگر توسعه داد. هدف اين مسئله اندازه‌گيري مساحت موجود براي گاوي است كه به خارج از سيلوي دايره‌اي بسته شده است. هافمن تصميم گرفت فضاي خارجي را نه‌تنها براي دايره، بلكه براي هر منحني مسطح ديگري از‌جمله بيضي و حتي منحني‌هاي غير‌بسته توسعه دهد.

اخيرا گراهام جيمسون، رياضي‌دان دانشگاه لنكستر، نمونه‌ي سه‌بُعدي مسئله‌ي داخل حصار را همراه‌با پسرش، نيكولاس، حل كرده است. ازآنجاكه بزها نمي‌توانند به‌راحتي در سه بُعد حركت كنند، جيمسون در مقاله‌ي سال ۲۰۱۷ اين مسئله را «مسئله‌ي پرنده» ناميد: اگر پرنده‌اي را داخل قفل كروي ببنديد، چقدر افسار يا بند لازم است تا پرنده بتواند به نيمي از حجم قفس دسترسي پيدا كند؟

با وجود تمام تغييرات، راه‌حل دقيق مسئله‌ي دوبُعدي داخلي حصار از سال ۱۸۹۴ مبهم باقي مانده بود تا اينكه اوليسچ در سال جاري راه‌حلش را ارائه كرد. او كار روي اين مسئله را در سال ۲۰۱۷ و پس از دريافت مدرك دكتري از دانشگاه مانستر آغاز كرد. اوليسچ به‌دنبال توسعه‌ي روشي جديد براي حل مسئله بود.

مسئله‌ي بز را مي‌توان به معادله‌اي غيرجبري تبديل كرد كه براساس تعريف، توابع مثلثاتي مثل سينوس و كسينوس را شامل مي‌شود؛ اما هدف اوليسچ تبديل مسئله به معادله‌اي رام‌شدني بود. او متوجه شد با استفاده از تحليل پيچيده مي‌تواند به چنين راه‌حلي دست پيدا كند. تحليل پيچيده شاخه‌اي از رياضيات است كه از ابزار تحليلي مانند حسابان براي توصيف اعداد پيچيده استفاده مي‌كند. رياضي‌دانان قرن‌هاست كه از تحليل پيچيده استفاده مي‌كنند؛ ولي اوليسچ اولين‌بار از اين روش براي حل مسئله‌ي بز گرسنه استفاده كرده است.

در رياضيات يافتن روش‌هاي جديد براي رسيدن به پاسخ ارزشمند است؛ حتي اگر مسئله قبلا حل شده باشد؛ زيرا مي‌توان مسئله را به روش‌هاي مختلفي تعميم داد.

هافمن قدري خوش‌بين‌تر است. معادله‌ي غيرجبري اوليسچ به معادلات غيرجبري هافمن در مقاله‌ي سال ۲۰۱۷ ربط دارند و هافمن با مطالعه مقاله‌‌ي سال ۱۹۵۳ به اين معادلات علاقه‌مند شد. او راه‌‌حل‌هاي موازي را‌ براي حل مسئله در انديشه متخصصين دارد و مي‌گويد:

تمام پيشرفت‌هاي علم رياضي از كشف‌هاي بنيادي سرچشمه نمي‌گيرند. گاهي با مطالعه روش‌هاي كلاسيك و يافتن زاويه‌اي جديد مي‌توان به نتايج جديد دست يافت.

مقاله‌ي اصلي با مجوز Quanta Magazine منتشر شد.